Special thanks go to Frank Schultz for numerous suggestions for comments and corrections.
General
The usage of the wavenumber ![]() is not consistent throughout the book. In many places
is not consistent throughout the book. In many places ![]() has to be replaced by
has to be replaced by ![]() since these two expressions are not fully equivalent:
since these two expressions are not fully equivalent: ![]() can become negative (such as in a Fourier transform, e.g., Eq. (B.4)) whereas
can become negative (such as in a Fourier transform, e.g., Eq. (B.4)) whereas ![]() , the length of the wave vector, is always non-negative. Eq. (2.3) equates the square of
, the length of the wave vector, is always non-negative. Eq. (2.3) equates the square of ![]() and
and ![]() for the same reason.
for the same reason.
Examples for expressions to which the replacement should be applied are Eq. (1.3) and (A.3). Note that the trace wavenumbers ![]() can indeed become negative.
can indeed become negative.
Another aspect to point out is the fact that ![]() is indeed the order of a Bessel or Hankel function. However, when it comes to associated Legendre functions and surface spherical harmonics, then
is indeed the order of a Bessel or Hankel function. However, when it comes to associated Legendre functions and surface spherical harmonics, then ![]() is termed the degree and
is termed the degree and ![]() the order.
the order. ![]() or
or ![]() may still be termed the maximum order of an expansion because
may still be termed the maximum order of an expansion because ![]() will never exceed
will never exceed ![]() (or
(or ![]() , respectively).
, respectively).
Page 7, Fig. 1.3
ITU-R BS.775 is a recommendation, not a standard.
Page 28, Fig. 2.4
Note that all subfigures are normalized such that the maximum is 1. Multiply (a) by 0.28, (b) by 0.35, (c) by 0.63, and (d) by 0.39 to undo the normalization.
Pages 31-32, Eq. (2.37)
The factor ![]() is missing on the left-hand side of Eq. (2.37a) and (2.37b).
is missing on the left-hand side of Eq. (2.37a) and (2.37b).
Page 39, Eq. (2.44)
The factor ![]() has to be removed from Eq. (2.44). (It turns the expansion upside down.) In order to normalize the look direction to 1, multiply by
has to be removed from Eq. (2.44). (It turns the expansion upside down.) In order to normalize the look direction to 1, multiply by ![]() . (Thanks to Mark R. P. Thomas for this hint.)
. (Thanks to Mark R. P. Thomas for this hint.)
Page 44, Fig. (2.13)
![]() shown on the horizontal axes in both subfigures is given in rad / m and not in rad.
shown on the horizontal axes in both subfigures is given in rad / m and not in rad.
Page 49, Sec. 2.3.1
I left out the letter “i” in several instances. The gentleman was called Dirichlet (as in the title of the section).
Page 49, Sec. 2.3.2
From Eq. (2.62) it is clear that ![]() is of unit length. This is not mentioned in the text (but assumed throughout the book).
is of unit length. This is not mentioned in the text (but assumed throughout the book).
Page 51, Eq. (2.67)
![]()
Note that Eq. (2.67) represents the directional gradient of a monopole source located in the coordinate origin.
Page 62, Eq. (3.15)
I reconsidered the formulation of Eq. (3.15), which is kind of sloppy in the book. A nicer representation is
(1) ![]()
![]() denotes the driving function of the secondary source located at
denotes the driving function of the secondary source located at ![]() .
. ![]() denotes the spatio-temporal transfer function of the secondary source at
denotes the spatio-temporal transfer function of the secondary source at ![]() . The proof that (1) does indeed constitute a spherical convolution follows below.
. The proof that (1) does indeed constitute a spherical convolution follows below.
Spherical convolution of two functions ![]() and
and ![]() is defined in (Driscoll and Healy 1994) as
is defined in (Driscoll and Healy 1994) as
(2) 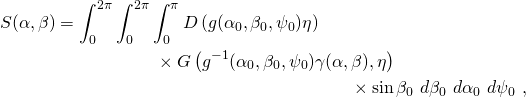
whereby ![]() represents a location on the unit sphere and
represents a location on the unit sphere and ![]() denotes the north pole of the latter. Using Euler matrix representation of rotation, the rotation matrix
denotes the north pole of the latter. Using Euler matrix representation of rotation, the rotation matrix ![]() can be written as
can be written as ![]() , whereby
, whereby ![]() and
and ![]() are
are ![]() matrices that represent counterclockwise rotations about the
matrices that represent counterclockwise rotations about the ![]() and
and ![]() axes, respectively.
axes, respectively.
(3) ![]()
holds. Eq. (2) can be rewritten to be (Rafaely 2004)
(4) ![Rendered by QuickLaTeX.com \begin{multline*} S( \alpha, \beta ) = \int_0^{2\pi} \int_0^{\pi} D \left( \alpha_0, \beta_0 \right) \\ \times \left[ \int_0^{2\pi} G \left( g^{-1}( \alpha_0, \beta_0, \psi_0 ) \gamma( \alpha, \beta ), \eta \right) d\psi_0 \right] \sin\beta_0 \ d\beta_0 \ d\alpha_0 \ , \ \ \ \ \end{multline*}](http://www.soundfieldsynthesis.org/wp-content/ql-cache/quicklatex.com-4f6a0b834315abf844bba5617bd114b9_l3.png)
where ![]() reduces to
reduces to ![]() . Assuming that
. Assuming that ![]() is invariant with respect to rotation about the
is invariant with respect to rotation about the ![]() axis, which is the case, e.g., when
axis, which is the case, e.g., when ![]() represents a monopole source at the north pole
represents a monopole source at the north pole ![]() of the sphere, then the inner integral in (4) evaluates to
of the sphere, then the inner integral in (4) evaluates to
(5) 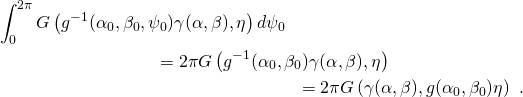
The latter equality only holds under free-field conditions, i.e., when a rotation of the coordinate system is equal to an according rotation of the source arrangement in opposite direction. Eq. (3.15) can thus be transformed to (3.17) under the given assumptions, whereby actually the factor ![]() has to be removed from (3.17) (and subsequent equations).
has to be removed from (3.17) (and subsequent equations).
Above derivation also points out why ![]() in (3) (and (3.17), respectively) represents the coefficients of the secondary source at the north pole as it is stated in the third bullet point on page 63.
in (3) (and (3.17), respectively) represents the coefficients of the secondary source at the north pole as it is stated in the third bullet point on page 63.
Page, 68, Eq. (3.27)
The summation over ![]() has to go from
has to go from ![]() to
to ![]() .
.
Page 91
The large argument approximation of the Hankel function is
![]()
Page 105, Eq. (3.101)
![]()
Page 170, Fig. 4.42
The sound field depicted in Fig. 4.42 exhibits a frequency of 1300 Hz and not 1000 Hz as stated in the caption.
Page 230, Sec. 5.7.1
The solution presented in this section is only valid if the source moves along the x-axis. Look here for an extension to arbitrary straight trajectories.
Page 231, Eq. (5.55)
The retarded time is actually defined as ![]() , i.e., it is the time that the sound source experiences with respect to the input signal.
, i.e., it is the time that the sound source experiences with respect to the input signal.
Page 231, Eq. (5.56)
There is an equals sign missing at the beginning of the second line of Eq. (5.56).
Page 233, Eq. (5.62)
The first case is valid for ![]() and
and ![]() .
.
